Ogólna teoria względności pokazuje, że obecność materii (gęstość energii) może zakrzywiać czasoprzestrzeń, co w efekcie powoduje ugięcie promieni świetlnych. Proces ten, zwany soczewkowaniem grawitacyjnym, w wielu przypadkach można opisać w sposób analogiczny do optycznego ugięcia światła przez (np. szklane) soczewki. Te interesujące własności światła i materii zostały wykorzystane w kosmologii. W większości sytuacji nie ma potrzeby rozwiązywania pełnego równania teorii względności, gdyż odchylenie czasoprzestrzeni spowodowane obecnością materii jest niewielkie. (Ilościowo masa taka porusza się powoli w stosunku do prędkości światła a wytwarzany potencjał grawitacyjny spełnia warunek 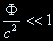 .)
.)
Schemat układu soczewkującego przedstawiony jest na rysunku: (oryginalny schemat)
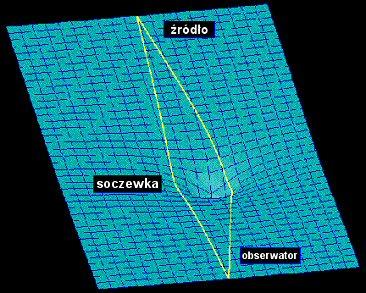
W układzie soczewkującym wyróżniamy:
źródło - miejsce, z którego wysyłane są promienie (może to być kwazar, mikrofalowe promieniowanie tła czy galaktyka)
soczewkę (soczewki) - które powodują ugięcie promieni świetlnych; ugięcie to jest tym większe, im większa jest masa/energia obiektu zakrzywiającego czasoprzestrzeń
obserwatora - który widzi bieg promienia świetlnego ugiętego na soczewce
obraz (obrazy) widziane przez obserwatora
Oprócz światła widzialnego, również inne rodzaje promieniowania elektromagnetycznego podlegają procesowi soczewkowania grawitacyjnego.
Konsekwencją takiego procesu jest fakt, że promienie, których obserwator nigdy by nie zarejestrował, dzięki odchyleniu w polu grawitacyjnym, mogą zostać zaobserwowane. Wyróżniamy następujące typy soczewkowania: silne, słabe i mikrosoczewkowanie. Różnice pomiędzy typami tego zjawiska zależą od pozycji źródła i soczewki względem obserwatora, jak również od masy i kształtu samej soczewki, które to własności decydują gdzie i jak bardzo promienie zostaną ugięte.
Silne soczewkowanie
Najsilniejsze ugięcie promienia świetlnego następuje w obecności bardzo masywnej soczewki, kiedy źródło promieniowania znajduje się blisko niej: wówczas światło może poruszać się wzdłuż wielu dróg w kierunku obserwatora, co powoduje powstanie wielu obrazów jednego obiektu. Pierwszym przykładem podwójnego obrazu, powstałego na skutek soczewkowania grawitacyjnego, był obraz kwazara obserwowany w 1979 roku.
Liczba odkrytych soczewek grawitacyjnych pomaga w oszacowaniu wielkości wszechświata odleglejszego od źródeł (wielkość ta zależy od parametrów kosmologicznych, w szczególności od stałej kosmologicznej).
Zmieniające się w czasie źródło decyduje o zmianach w obserwowanych obrazach. Mimo to, odległości, jakie pokonują np. dwa promienie świetlne i w wyniku ugięcia przestrzeni powodują powstanie dwóch różnych obrazów, nie są jednakowe. W rezultacie pojawia się różnica w czasie pomiędzy zmianami w obserwowanych obrazach. Takie opóźnienie wykorzystywane jest do obliczania wartości stałej Hubble'a.
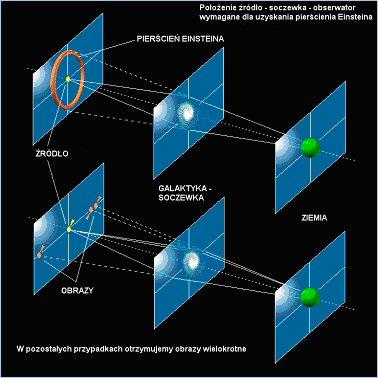
W szczególnych przypadkach położenie soczewki i źródła pozwala zaobserwować charakterystyczny obraz, tzw. "pierścień Einsteina". Częściej jednak zamiast pierścienia widzimy łuki świetlne. Do wytworzenia łuku (pierścienia Einsteina) masa źródła musi być bardzo duża, zatem własności łuków (ich liczba, rozmiar, kształt) pozwalają badać masywne obiekty np. gromady galaktyk.
Na poniższym schemacie ukazany jest sposób formowania się pierścienia Einsteina i obrazów wielokrotnych: (schemat oryginalny)
Słabe soczewkowanie
W wielu przypadkach soczewka nie jest wystarczająco silna (zbyt mała masa/gęstość), aby utworzyć obrazy wielokrotne czy łuki świetlne. Mimo to, obserwowane źródło pozostaje zniekształcone (wzmocniony i ścięty obraz). Jeśli posiadamy pełne dane o rozmiarach i kształtach źródeł, badając zniekształcenie obrazu możemy otrzymać konkretne własności soczewki (rozmiar, masa, gęstość).
Zazwyczaj nie dysponujemy wystarczającymi informacjami o źródłach; wówczas posługujemy się tylko danymi szacunkowymi rozkładu masy dużej struktury (gromady galaktyk, supergromady). Sposób postępowania jest następujący: badając charakter zniekształcenia obrazu (ścięcia) można zmierzyć siłę pola grawitacyjnego soczewki, a następnie określić jej masę. Słabe soczewkowanie grawitacyjne może być zatem wykorzystane również do wyznaczania masy ciemnej materii (ciemna materia, chociaż jej nie widzimy, oddziałuje grawitacyjnie na promienie wysyłane przez źródło).
Mikrosoczewkowanie
W niektórych przypadkach soczewkowanie jest na tyle słabe, że niemożliwe jest zaobserwowanie obrazu źródła, a jedynie dodatkowe promienie świetlne ugięte w wyniku działania pola grawitacyjnego soczewki. Pozwala to zarejestrować jaśniejszy obraz źródła. Sposób ten pozwala więc rejestrować obiekty, które dotychczas były niewidoczne lub bardzo odległe. Soczewką jest zazwyczaj mało masywny obiekt, np. gwiazda.
Mikrosoczewkowanie wykorzystuje się również do poszukiwania typu ciemnej materii zwanego MACHO (massive compact halo objects), czyli zwartych masywnych obiektów halo, budujących naszą Galaktykę. Ponieważ nie można ich zaobserwować bezpośrednio, poszukuje się pobliskich źródeł chwilowo (np. kilka dni, tygodni) zwiększających swoją jasność. Naukowcy twierdzą, że przynajmniej połowa ciemnej materii w Drodze Mlecznej to struktury MACHO.
Innym zastosowaniem mikrosoczewkowania grawitacyjnego jest poszukiwanie planet poza Układem Słonecznym (pomysł i metoda opracowane przez dr Bohdana Paczyńskiego).
Zdjęcie pokazuje gromadę galaktyk Abell 2218 wraz z efektami silnego soczewkowania (łuki świetlne i obrazy wielokrotne) (źródło)

Przykład silnego soczewkowania grawitacyjnego: galaktyka - soczewka (kolor żółty) powoduje ugięcie promienia z odległego kwazara (niebieskie bąbelki) dając poczwórny obraz na niebie. Jeśli jasność kwazara zmienia się w czasie, wówczas dzięki obserwacji możliwe jest zmierzenie szybkości ekspansji wszechświata. Ponadto zmiany pozycji obrazów kwazara pomagają w określeniu masy soczewki.(źródło)

Źródło: http://www.joannad.nazwa.pl/universe/index2.php?file=5&sec=gal