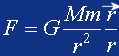PRAWO POWSZECHNEJ GRAWITACJI
W XVII w. Izaak Newton odkrył prawo powszechnej grawitacji. Określa ono wielkość siły oddziaływania między dwoma, posiadającymi masy (m i M) oddalonymi od siebie o r. Prawo to mówi:
Prawo powszechnego ciążenia
Siła oddziaływania grawitacyjnego między dwoma ciałami jest wprost proporcjonalna do iloczynu tych mas i odwrotnie proporcjonalna do kwadratu odległości między nimi:
G jest stałą fizyczną zwaną stałą grawitacji
G = 6,67 . 10-11 N . m2 / kg2
Jak więc widać z tego wzorku, wszystkie ciała posiadające masę przyciągają się nawzajem. Słońce przyciąga planety, Ziemia przyciąga Księżyc, a monitor komputera, przed którym najprawdopodobniej siedzisz przyciąga ciebie :)
Jeśli chcesz się przekonać jakimi siłami przyciągają się poszczególne ciała, policz sobie, albo zajrzyj do zadań.
NATĘŻENIE POLA GRAWTIACYJNEGO
Jeśli chcemy porownać dwa pola grawitacyjne albo dwa punkty tego samego, niejednorodnego pola grawitacyjnego powinniśmy znać jakieś cehy tego pola. Jedną z takich cech jest natężenie pola grawitacyjnego, które wyraża się wzotrem
γ = F / mZatem natężenie pola grawitacyjnego jest to iloraz siły działającej na ciało o masie m przez tę masę. Jak łatwo się domyślić, jednostką natężenia pola grawitacyjnego jest N / kg
Od czego zależy natężenie pola grawitacyjnego? Na pierwszy rzut oka można dojść do wniosku, że od siły działającej na ciało i jego masy. A od czego zależy siła? Pisałem wcześniej o prawie powszechnej grawitacji, przypomnij sobie!
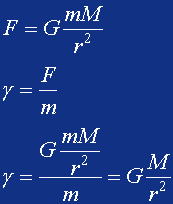 Z tej zależności widać bezpośrednio, że natężenie pola grawitacyjnego w danym punkcie zależy od masy ciała, które te pole wytwarza oraz od odległości tego punktu od tej masy.
Z tej zależności widać bezpośrednio, że natężenie pola grawitacyjnego w danym punkcie zależy od masy ciała, które te pole wytwarza oraz od odległości tego punktu od tej masy. Na lekcjach zdarza się czasem, że trzeba sporządzić wykres natężenia pola grawitacyjnego lub siły działającej na masę m w zależności od odległości od środka np. Ziemi. Wykresy te sporządza się tak samo, nie trudno się chyba domyślić, dlatego zrobię to na przykładzie wykresu F(r).
Jeśli chodzi o wykres od R (promień Ziemi) do nieskończoności nie ma problemu, ponieważ z prawa powszechnej grawitacji widać, że siła jest odwrotnie proporcjonalna do kwadratu promienia, a więc mamy do czynienia z hiberbolą. Sprawa komplikuje się przy rysowaniu wykresu od środka Ziemi do jej powierzchni. Załóżmy, że w Ziemi wydrążono tunel przechodzący przez jej środek. Jakie będzie siła grawitacji działająca na masę m np. w punkcie oddalonym od środka planety o 1/2 R ?

Z rysunku widać, że siła ta będzie równa sile grawitacji działającej na tą masę przez planetę o promieniu 1/2R. (oczywiście zakładamy, że gęstość Ziemi jest wszędzie jednakowa). Zatem obecną masę, która wytwarza pole zapisujemy jako M'. Możemy ją obliczyć mając gęstość i znając wzór na objętość kuli. Znajdźmy zatem zależność F(r):

Widać zatem, że wewnątrz planety szukana zależność jest liniowa.
PRAWA KEPLERA
Pierwsze prawo Keplera
Planety krążą po orbitach eliptycznych, a jednym z ognisk elipsy jest Słońce
Drugie prawo Keplera
Pola powierzchni wycinków elipsy zakreślone przez promień wodzący planety w jednakowych przedziałach czasu są jednakowe.
Prawo to obrazuje rysunek:

Zgodnie z II prawem Keplera, zaznaczone na szaro pola są równe. Wynika z tego, że prędkość V2jest mniejsza niż V1.
Trzecie prawo Keplera
Dla każdej planety Układu Słonecznego stosunek sześcianu średniej odległości od Słońca do kwadratu okresu obiegu wokół tej gwiazdy jest stały.
Brzmi to może troszeczkę skomplikowanie, ale myślę, że wszystko wyjaśni się, jeśli to prawo wyprowadzimy.
Rozpatrujemy planetę, która porusza się w polu grawitacyjnym Słońca: m - masa tej planety
M - masa Słońca
r - odległość tej planety od Słońca
T - okres obiegu planety wokół Słońca
zakładamy, ze planeta porusza się po okręgu, zatem siła dośrodkowa jest równa sile oddziaływania grawitacyjnego między tymi planetami:

Z ruchu po okręgu możemy obliczyć prędkość:

Otrzymaliśmy więc III prawo Keplera ponieważ G,M są stałe, zatem stosunek sześcianu promienia do kwadratu okresu obiegu jest stały. Jest to tak zwane nieuogólnione III prawo Keplera.
Teraz zagadnienie nico trudniejsze, wyprowadzimy uogólnione III prawo Keplera. Będzie tu trochę więcej matematycznych przekształceń i kilka ciekawych pojęć fizycznych.
Zakładamy, że planeta o masie m i gwiazda o masie M krążą wokół ich wspólnego środka masy O tak jak na rysunku:

a = a1 + a2 - odległość między planetą, a gwiazdą
v1 - prędkość liniowa gwiazdy
v2 - prędkość liniowa planety
T - okres obiegu planet wokół ich wspólnego środka masy.
Wiemy, że w obudwu przypadkach siła dośrodkowa jest równa sile grawitacji, prędkość można wyznaczyć z ruchu po okręgu, a plantey poruszają się po orbitach o promianiach a1 i a2:

Po odpowiednim podstawieniu i skróceniu otrzymujemy układ równań, który następnie dodajemy stronami:

Po odpowiednim przekształceniu otrzymujemy III prawo Keplera uogólnione

Z uogólnionego III prawa Keplera bardzo łatwo wyprowadzić prawo nieuogólnione, wystarczy zapisać uogólnione prawo dla 2 planet, a następnie podzielić stronami. Następnie założyć, że masy planet względem masy Słońca są pomijalnie małe i otrzymać:

Źródło: http://www.superfizyka.za.pl