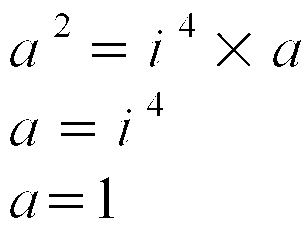SUPERLICZBY! Liczby Grassmanna. Jakie mają właściwości? Co nowego przed nami odkryją?
SUPERLICZBY
Superliczby to liczby Grassmanna. Można powiedzieć, że wymnożenie superliczb w uproszczonej formie, czyli takiej, że superliczba wymnożona przez taką samą superliczbę, zachowuje dla nas dziwne własności. Otóż wymnożenie takiej struktury jest równe wymnożeniu takiej samej struktury, tylko, że o znaku przeciwnym. Również jest taka możliwość, dzięki powyższej własności, że superliczba jest równa 0. Powyższe wnioski możemy wysnuć z treści i wzorów zawartych w rozdziale „Błędy i urojenia w matematyce”. Tam też wspomnieliśmy o tym, że takie własności nie mieszczą się w zbiorze liczb rzeczywistych. Czy jest możliwe, aby superliczby były nowym zbiorem liczb?
Przypomnijmy przytoczony we wstępie wzór właściwy dla liczb urojonych:
a = -1/a
Wiemy już ze wstępu, że nasza zmienna a jest liczbą urojoną i.
i = -1/i
Jest to przykład, który ukazuje strukturę nieskończonych działań, coś co było dla mnie pierwszym odkryciem i zaskoczeniem.
Możemy również zrobić coś podobnego dla superliczb. Tym razem musimy znaleźć inną własność, która jest charakterystyczna dla superliczb.
W poprzednim przykładzie wykorzystaliśmy mechanizm dzielenia w struktrze, która składała się z nieskończonej ilości elementów i to nas doprowadziło do liczby urojonej, która jest poza zbiorem liczb rzeczywistych. Tym razem nie możemy użyć dzielenia. Dlaczego?
Bo już szliśmy tą drogą i coś osiągnęliśmy, a teraz chcemy osiągnąć inną jakość. Trochę nam podpowiada wynik, gdzie mamy szukać nowej jakości. Wynikiem jest liczba urojona i. To jest pierwiastek z -1. A więc spróbujmy zastosować ów pierwiastek jako nasze nowum.
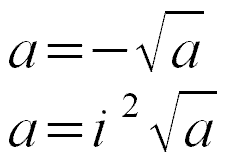
Mamy tu 2 wzory, które są sobie równe, ponieważ:
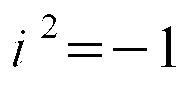
Możemy obliczyć również zmienną a na 2 różne sposoby. Oto pierwszy z nich:
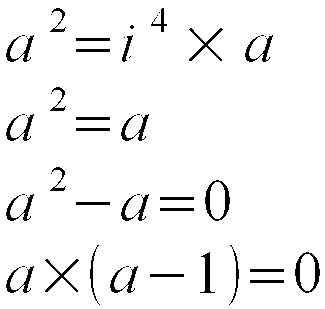
Na początku podnieśliśmy obie strony do kwadratu. Potem przenieśliśmy prawą stroną równania na lewą stronę i wyciągnęliśmy przed nawias część wspólną.
Mamy tutaj 2 rozwiązania równania:
a 1 = 0 i a 2 = 1.
Niby nic odkrywczego, ale...
Pokrywa nam się własność superliczb, że są równe 0. Co do drugiego wyniku, to spróbujemy do niego dojść obliczając zmienną a w drugi sposób, inną metodą:
W drugim sposobie obliczania zmiennej a musimy założyć, że zmienna a jest różna od 0. Dzielimy bowiem obie strony równania przez zmienną a. Gdyby zmienna a była równa 0, to wynikiem takiego działania byłaby liczba nieokreślona, a tego chcemy uniknąć. Tak więc doszliśmy do takiego samego rozwiązania, jak w pierwszym sposobie rozwiązywania, ale nasze założenie odrzuca rozwiązanie, że zmienna a = 0, ale jest równa drugiemu rozwiązaniu z pierwszego sposobu obliczania zmiennej a.
Jak widzimy obliczenie superliczby nie jest łatwe. Dzieje się tak ponieważ superliczby są poza zbiorem liczb rzeczywistych i nawet, gdy je obliczamy w tradycyjny sposób pojawia się zakaz dzielenia przez 0 i coś nowego: i 4.
W takim razie musimy udowodnić jeszcze raz, że superliczby to jest właśnie: i 4. Ale nasz cel, znalezienie superliczb, został w połowie osiągnięty, doszliśmy do pewnej nowej, nieznanej nam struktury, która upraszcza się nam do 1. Jest tu obecne coś, co znamy i nie znamy zarazem, gdyż coś co znamy, zasłania nam to, czego jeszcze nie znamy. Odkrywanie starych rzeczy na nowo, staje się domeną poznania jeszcze bardziej zaawansowanych rzeczy nowych.
Ta struktura ma swoją nieskończoną reprezentację we wzorze nieskończonych działań:
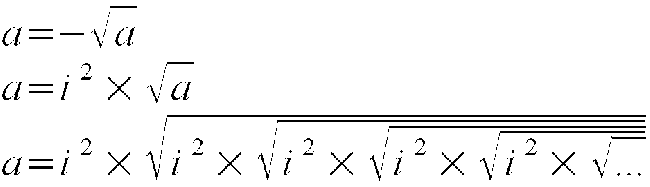
Jest to zadziwiająca struktura, która nam odsłania nową własność superliczb. Jak widzimy takich możliwości nie mają liczby rzeczywiste, również nie mają liczby urojone. A więc superliczby nie mieszczą się w tych zbiorach, wykraczają poza nie.
Musimy jeszcze udowodnić, że i 4 jest superliczbą i spełnia następujący warunek:
a * a = - a * a
Tym razem za a musimy podstawić i 4. Nie będzie to łatwe, bo musimy w naszych dowodach wzbić się ponad nasze zdolności matematycznego rozumowania, aby znowu zrozumieć rzeczy nowe.
i 4* i 4 = - i 4* i 4
Oto dowód:
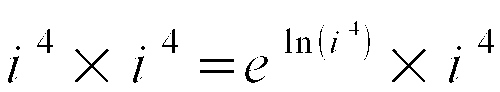
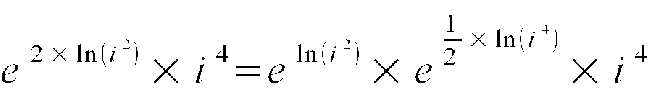
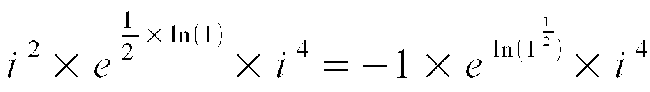
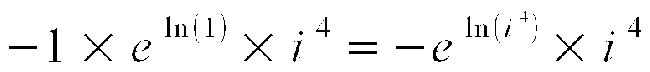
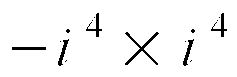
Czyli:
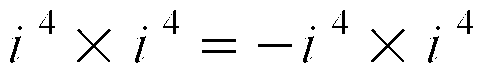
Ażeby udowodnić, że i 4 jest superliczbą, musieliśmy użyć funkcji logarytmu naturalnego, liczby e, która jest podstawą tego logarytmu i funkcji potęgowych oraz przekształceń z i 4 na 1 oraz z i 2 na -1.
Również jest tu wykorzystana możliwość zamiany potęgi liczby logarytmowanej na postać iloczynu z
logarytmem. Jest tu trochę liczb urojonych, ale jest też logarytm naturalny z 1. Taka postać logarytmu
może być równa 0, ale nie tylko. Istnieje nieskończenie wiele rozwiązań takiego logarytmu
naturalnego z 1. Począwszy od 2 * π * i, dalej 4 * π * i, 6 * π * i, 8 * π * i, aż po
wielokrotność wyrażenia 2 * n * π * i, gdzie n jest liczbą naturalną i może być bardzo dużą liczbą
naturalną. Również nieskończoność ∞ jest rozwiązaniem tego równania. Wchodzimy z
superliczbami w matematykę wyższych wymiarów, gdzie rozwiązań jest nieskończenie wiele. To co
znamy, przesłania nam to, czego nie znamy i dlatego odrzucamy rzeczy nowe. Tylko wtedy nie
zrozumiemy, czym są superliczby, skąd się wzięły i jakich wymiarów dotyczą. Powyższy dowód zawiera
jeszcze jedną dodatkową trudność, która wynika z logarytmowania liczb ujemnych. W równaniach wartością
logarytmowaną, jak wspomniałem wcześniej jest i 2. Jest to wartość ujemna, która z
definicji logarytmu, nie powinna się pojawić. Uważam, że możemy przekroczyć ten zakaz ze
względu na własność supersymetrii, która występuje w superliczbach i ten minus w logarytmie jest
jednocześnie plusem, bo tak działa własność supersymetrii. Niestety, aby wyjść z ograniczeń,
musimy przekroczyć pewien zakaz. Podobnie było z liczbami urojonymi i dzisiaj nie przeszkadza nam
pierwiastkowanie liczb ujemnych. Dzięki temu dużo zyskaliśmy w matematyce, więc i dzięki
superliczbom zyskamy nowe zrozumienie, tylko musimy się na nie otworzyć i zaakceptować fakt
przekroczenia pewnego małego zakazu. Udowodniliśmy, że superliczby istnieją i mają swoją
strukturę, którą potrafimy wyrazić. Oparliśmy się o własności liczb urojonych i to nas doprowadziło do
nowej jakości.
Ostatecznie musimy znieść tylko jeden zakaz, ale bez tego nie ma rozwoju. Przypuszczam, że część
czytelników zatrzyma się na tym etapie, ze względów formalnych i odrzuci część moich
dowodów. Tych wszystkich, którzy mają otwarte umysły i szerokie horyzonty myślowe, zapraszam
serdecznie do dalszych treści tego opracowania, gdyż będziemy penetrować wyższe wymiary jeszcze
głębiej i jeszcze dokładniej, a to może być jeszcze bardziej fascynujące niż to, co znamy.
C.D.N.