PRATIQUE DES ETUDES DE RENTABILITE DE PROJETS D'INVESTISSEMENT

AVANT-PROPOS

1. NOTION DE BASE: LA VALEUR ACTUELLE DE REVENUS FUTURS

2. LA METHODE DU TRI
L'excédent brut d'exploitation
Taux de rentabilité interne (TRI)
Appréciation du tri obtenu par rapport à une référence
Comparaison de projets selon le critère du TRI
Etudes de sensibilité
Limites du TRI

3. LA METHODE DE LA VALEUR ACTUELLE NETTE
La valeur actuelle nette
Comparaison de projets selon le critère de la VAN
Limites de la méthode de la VAN

4. LA METHODE DU TABLEAU FINANCIER

5. LA METHODE DU TEMPS DE RETOUR SUR INVESTISSEMENT ET DU TAUX DE RENTABILITE EXTERNE
Temps de retour sur investissement
La méthode du taux de rentabilité externe

6. SYNTHESE DES METHODES DU TRI ET DE LA VAN
Rappel de la méthode du TRI
Rappel de la méthode de la VAN
Calculs manuels et simplifiés
Faut-il maximiser le TRI ou la VAN ?
Représentation graphique
Exemple pratique

7. RENTABILITE ECONOMIQUE D'UN PROJET
71. Valeur ajoutée et balance des paiements
72. Correction des distorsions de prix
73. Balance des paiements du projet

AVANT-PROPOS

Les entreprises sont au coeur des activités de production de tous les biens et services que les sociétés humaines consomment pour satisfaire leurs besoins. Selon l'histoire du développement des différentes communautés, organisées en Etats et dotés d'organisations sociales économiques et juridiques propres, la nature et le mode de fonctionnement de ces entreprises varient sur le plan "institutionnel". Il y a ainsi des entreprises privées et des entreprises publiques.

Voir document "Comment l'étude des structures industrielles peut-elle être scientifique ?

Pendant une grande partie du 20ème siècle, et principalement pendant les 4 décennies qui ont suivi la fin de la deuxième guerre mondiale entre les nations démocratiques groupés autour de la Grande Bretagne, les Etats Unis et la France d'une part, l'URSS d'autre part, en guerre avec l'Allemagne et le Japon, le monde était divisé en deux camps idéologiques: le capitalisme et le communisme. Un "rideau de fer" séparait les deux camps et ceux-ci s'affrontaient sur les plans militaire et économique pour exercer leur influence dans différentes parties du monde. C'était la "guerre froide", car on n'était pas tout à fait en guerre, mais les deux camps exerçaient une "course aux armements", toujours plus perfectionnés, pour assurer leur sécurité et leur hégémonie. C'est dans ces conditions que les Etats-Unis ont pris la tête du camp capitaliste et ont acquis aujourd'hui une position dominante dans la plupart des domaines: scientifique, technologique, militaire et économique.

Au cours du 20ème siècle, les activités de production de biens et services se sont considérablement accrues, particulièrement dans les dernières décennies du siècle après la fin de la deuxième guerre mondiale. On peut parler d'une véritable explosion dans tous les domaines: scientifique, technologique, économique et militaire. Cette explosion des activités s'est produite principalement dans les pays d'Europe occidentale sous l'impulsion des Etats-Unis, dans ses extensions ex-colonies de peuplement, que sont les Canada, l'Australie, la Nouvelle Zélande, et aussi le Japon et les pays de l'Asie du Sud-Est.

A la fin des années 1980, l'Union Soviétique, bâtie par 70 ans de communisme s'effondra et rejoignit le camp du capitalisme et de l'économie de marché. Depuis lors, les conditions sont propices pour l'extension mondiale de l'économie de marché. Et on assiste aujourd'hui à l'explosion économique de la Chine et de l'Inde d'une part et au phénomène de la "mondialisation", c'est à dire de la volonté de participation d'un nombre croissant de pays à l'économie de marché, les entreprises pouvant installer des usines et des ateliers de fabrication partout dans le monde. Lors de la guerre froide, ceci était quasiment impossible; les entreprises des pays capitalistes ne pouvaient pas s'établir dans des pays sous influence communiste. Exemple, la Tanzanie, ou l'Inde au moment de la politique d'import substitution ou du schéma de développement autocentré des "collaboration agreements"...

Quelque soit le régime politique qui fixe les règles de fonctionnement économique, toutes les entreprises sont confrontées à des contraintes. Il s'agit d'abord du volume de la production et des prix de vente, de la qualité et de la durée de vie des produits, mais aussi des matières premières et des consommations intermédiaires nécessaires, des autres facteurs de production dont la main d'oeuvre et les charges sociales, des technologies mises en oeuvre et de l'évolution de celles-ci avec la recherche et développement et l'innovation.

Toute cette croissance économique a été motivée par la recherche d'amélioration de la qualité de vie en matière de santé, d'éducation, de bien-être matériel, de loisirs, etc... pour les populations. Sur le plan technique cela concerne le développement de la production d'énergie, électricité et pétrole, les transports: routiers, ferroviaires, aériens et maritimes, et leurs infrastructures, les équipements ménagers et de loisirs, l'informatique et les communications... Ces progrès ont nécessité l'extraction croissante de ressources minières de toutes sortes: énergétiques (charbon, lignite, pétrole, uranium), fer et ses métaux d'alliage, métaux non ferreux (cuivre, plomb, zinc, étain), métaux précieux (or, argent, platine, palladium), phosphates potasses et sels, et bien d'autres encore notamment les minéraux industriels (calcaires, chaux, kaolins, argiles).

Pour atteindre des objectifs de production d'un bien, en volume, en qualité et en durée de vie c'est à dire de manière durable, et contribuer ainsi à satisfaire les besoins du marché pour ce bien, sans appauvrissement c'est à dire sans consommer des ressources de la collectivité produites par ailleurs mais au contraire en les augmentant, l'entreprise a besoin d'être rentable économiquement, c'est à dire qu'elle doit d'abord assurer l'équilibre de ses dépenses et de ses recettes.

Cette rentabilité résulte de la confrontation de l'ensemble de tous les coûts, et des revenus générés par la vente de la production sur le marché, au prix fixés par celui-ci, dans le cadre de l'équilibre entre la demande et l'offre, et de la concurrence avec les éventuels producteurs du même bien, lesquels peuvent avoir des coûts différents et donc être capables d'accepter un prix de vente différent. Le prix de marché s'établit alors par la confrontation des offres des producteurs avec des demandes des utilisateurs, jusqu'à obtenir un équilibre des transactions.

Dans le domaine minier qui nous intéresse ici, ces mécanismes sont bien connus maintenant. L'exemple le plus typique est celui du cuivre auquel je me réfèrerai le plus souvent.

L'évaluation de la rentabilité d'un projet d'investissement sur une période d'évaluation définie en nombre d'années, peut se faire de plusieurs manières qui seront examinées ci-après:

la méthode du taux de rentabilité interne (TRI) du capital investi dans le projet
la méthode de la valeur actuelle nette (VAN) de la marge dégagée par le projet;
la méthode du tableau financier simule les comptes financiers du projet de manière comptable et aboutit au tableau des sources et emplois de fonds dont le solde est le cash-flow net; c'est le surplus monétaire qui est à la disposition de l'entreprise et qui lui permet d'assurer la rémunération du capital propre des propriétaires, son équilibre financier et sa croissance;
la méthode du temps de retour sur investissement (payback period) et du taux de rentabilité externe;
on examinera dans une cinquième section la synthèse des méthodes du TRI et de la VAN
enfin, la rentabilité économique d'un projet pour l'économie d'un pays, sera abordée en section 6.

retour sommaire

1. NOTION DE BASE: LA VALEUR ACTUELLE DE REVENUS FUTURS

Pour la bonne compréhension des notions économiques qui suivent, il est nécessaire de définir ce qu'on entend par valeur actuelle (VA) d'un revenu futur et par valeur actuelle nette (VAN) d'une série de revenus annuels futurs.

La valeur actuelle (VA), c'est à dire à l'année 1, d'un revenu de 100 M$ attendu par exemple à l'année 8, est le montant du capital qu'il faut placer l'année 1, à intérêts composés, pour disposer l'année 8, d'un montant capital et intérêts, de 100 M$. Pour un taux d'intérêt de 8% par exemple, la VA d'un revenu de 100 M$ reçu l'année 8 est de 54 M$. Cette VA est de 31.5 M$ pour le même revenu reçu l'année 15 ou de 21.5 M$ s'il est reçu l'année 20. La VA d'un revenu futur est donc de plus en plus faible pour les revenus plus lointains dans le temps, puisque le taux d'intérêt joue pendant plus longtemps.Voir figure.

Il en est de même en ce qui concerne le taux de l'intérêt; plus l'intérêt est élevé moins il faut placer de capital l'année 1. Voir figure: les valeurs précédentes deviennent respectivement 40.4 M$ 18.3 M$ et 10.4 M$.

NB: par convention, on considère que le capital est placé au 1er janvier de l'année et que le revenu est reçu le 31 décembre de l'année. Ainsi 92.6 M$ placés le 1er janvier de l'année 1 à 8%, donnent un revenu de 100 M$ le 31 décembre de l'année 1 (92.6 +8%=100). Voir figure.

La valeur actuelle nette (VAN) d'une série de revenus futurs au taux d'intérêt de 8% par exemple (VAN 8%), est la somme des valeurs actuelles de la série des revenus ou marges annuels escomptés d'un projet. C'est le montant qu'il faut placer l'année 1 pour bénéficier de la série des revenus annuels, par exemple 100M$ tous les ans pendant 20 ans soit 2000M$ non actualisés. Pour un taux d'intérêt de 0%, la VAN 0% est égale à la somme arithmétique de la série des marges annuelles soit 2000M$ . Plus le taux d'intérêt est élevé, plus la VAN est faible puisque la VA des revenus les plus lointains dans le temps est de plus en plus faible. Ainsi pour la série de 100M$ sur 20 ans et 8% d'intérêt, la VAN est 982M$; donc en plaçant 982M$ l'année 1, on obtient 100M$ tous les ans pendant 20 ans. Voir figure.

Dans le cas de 12% d'intérêt, la VAN devient 747M$, c'est à dire qu'il faut placer 235M$ ou 24% de moins. Voir figure.

En sens inverse, appliqué à un projet ou à une entreprise, on dira qu'en investissant 747 M$ l'année 1 et en obtenant un revenu annuel de 100 M$ pendant 20 ans, c'est comme si on avait un taux d'intérêt de 12%. Et qu'en investissant 982 M$ l'année 1 et en obtenant ce même revenu annuel de 100 M$ pendant 20 ans, c'est comme si on avait un taux d'intérêt de 8%. Il est clair que le taux de 12% est plus intéressant que 8% soit 4 points de plus, puisqu'on obtient les mêmes revenus annuels en investissant 235 M$ ou 24% de moins.

On désigne aussi le taux d'intérêt adopté pour ces calculs sous le nom de taux d'actualisation. Ce terme est en effet plus approprié, dans la mesure où le taux d'intérêt désigne plus précisément le coût de l'argent sur le marché monétaire, dans des conditions économiques et à un moment donnés.

Télécharger le fichier excel de cette section (va.xls).Une fois téléchargé, tu pourras le sauvegarder sur ton disque dur.

retour sommaire

2. LA METHODE DU TAUX DE RENTABILITÉ INTERNE (TRI)

C'est la méthode la plus simple, la plus rapide et la plus significative sur le plan économique. Elle consiste à établir le flux des revenus futurs, c'est à dire la différence entre les recettes provenant des ventes de la production selon le programme prévu et les coûts directs c'est à dire les coûts d'intrants et du personnel; puis à établir les montants des capitaux d'investssements initiaux nécessaires.

L'excédent brut d'exploitation

On calcule l'excédent brut d'exploitation ou la marge brute d'exploitation dégagée par le projet année par annéz (voir la structure des comptes d'une entreprise dans le diagramme ci-après. C'est la différence entre la production annuelle vendue aux prix du marché et le coût direct d'exploitation annuel qui est constitué par les intrants (consommations et achats extérieurs), le coût du personnel, les frais généraux, les impôts directement liés à la production (redevances et royalties calculées en fonction des tonnages ou de ventes etc.).

On constitue alors un échéancier constitué en premier par la marge brute annuelle dégagée, en deuxième par les dépenses d'investissement du projet; on calcule alors en troisième lieu la marge nette ou cashflow c'est à dire la différence entre la marge brute annuelle et l'investissement.

L'investissement est une dépense exceptionnelle importante que l'on doit consentir pour une durée de plusieurs années et qui ne se répète pas annuellement. Si l'on s'interroge sur la rentabilité d'un investissement, on pourra considérer comme période d'évaluation, la durée de vie technique et économique de cet investissement.

Taux de rentabilité interne (TRI)

Le taux de rentabilité interne (TRI) est le taux d'actualisation X%, tel que la valeur actuelle nette de la série des revenus annuels (ou marges brutes) dégagées par le projet, est égale à l'investissement initial; la VAN des revenus futurs à taux d'actualisation X% = l'investissement initial). Autrement dit, la VAN à X%, de la série des marges annuelles brutes, représente la valeur de l'investissement nécessaire pour obtenir cette série de revenus futurs annuels.

Si on raisonne sur la marge nette ou le cashflow, le TRI est le taux d'actualisation tel que la valeur actuelle nette de la série des marges nettes ou cashflow annuels, est égale à zéro.Voir figure qui montre les TRI de deux projets, l'un de 200M$ d'investissement initial répartis sur 2 ans et 55M$ de revenus annuels sur 20 ans (projetA), l'autre de 150M$ d'investissement initial répartis sur 2 ans et 20M$ de revenus annuels sur 20 ans (projetB).

Méthode et exemples de calcul du TRI

Par exemple, pour le projet (A) dont l'investissement initial est de 150 millions US$ dépensés la première année, 200 millions US$ la deuxième année et la marge brute annuelle est de 55 millions US$ pendant 20 années à partir de l'année 3, la VAN 8% est 153 M$ et le TRI est de 13.8%.Voir figure.

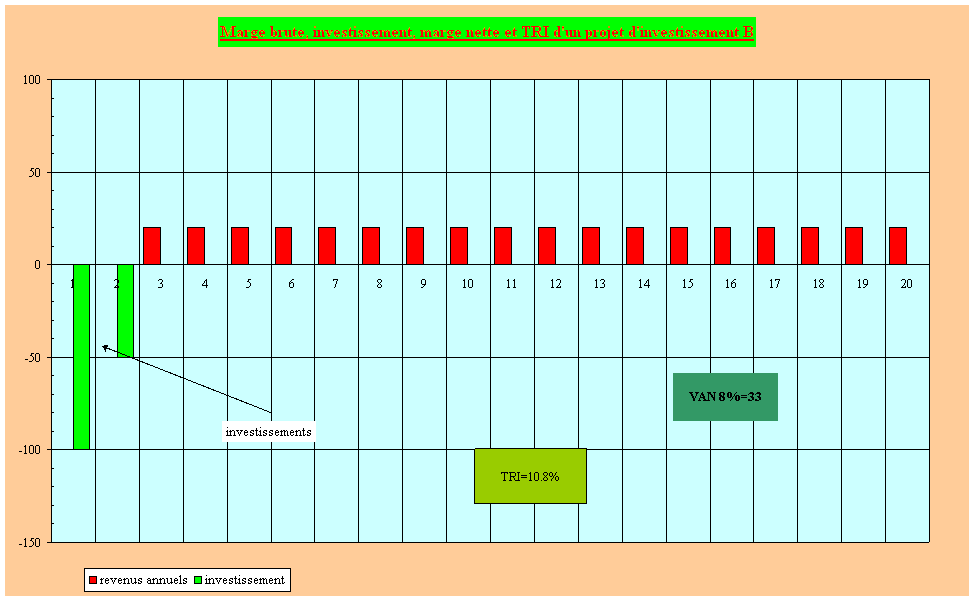
Pour le projet B dont l'investissement initial est de 100 millions US$ dépensés la première année, 50 millions US$ la deuxième année et la marge brute annuelle est de 20 millions US$ pendant 20 années à partir de l'année 3, la VAN 8% est 33 M$ et le TRI est de 10.8%.Voir figure

Les deux projets sont comparés de la manière suivante: Voir Figure.

On peut aussi représenter sous forme de courbe la variation de la VAN de chaque projet en fonction du taux d'actualisation croissant. Le TRI correspond à l'intersection de la courbe avec l'axe des abscisses (VAN=0 pour cette valeur). Voir Figure.

Appréciation du tri obtenu par rapport à une référence

TRI de référence

Le TRI obtenu doit ensuite être apprécié; est-il bon ou pas et de combien? Pour cela, on le compare à un taux d'intérêt de référence que l'on désigne sous le nom de taux d'opportunité du capital. C'est le taux auquel les ressources financières (les capitaux) sont disponibles sur le marché monétaire au moment de la réalisation du projet, c'est à dire de l'engagement des investissements. On considère que les investissements vont être constitués de fonds propres non rémunérés, et d'emprunts contractés auprès d'institutions financières. Le rôle de celles-ci est en effet de stimuler le l'activité économique. Les fonds collectés par ces institutions proviennent de diverses sources dont les entreprises et les particuliers disposant de liquidités pour lesquelles ils attendent une rémunération sous forme d'intérêt.

Comme les calculs sont faits en monnaie constante c'est-à-dire sans tenir compte d'inflation des prix et des coûts sur la durée de vie du projet, il faut apprécier dans le taux du marché monétaire, quelle est la part qui correspond à l'estimation du risque d'inflation. C'est le facteur d'incertitude de l'avenir estimé par le marché, pour le moyen et le long terme. Cette appréciation se fait sur la base des taux pratiqués sur les différents marchés financiers des pays de l'OCDE, de la lecture des journaux économiques et des prévisions qui y sont faites. C'est ainsi qu'en 1995, les taux pratiqués en Allemagne et en France étaient de l'ordre de 6% avec une prévision d'inflation de 2.5%, ce qui donnait un taux d'intérêt en termes réels de 6.0-2.5=3.5%.

Ce taux correspond à la rémunération du capital en monnaie constante en 1995. C'est le prix à payer par des investisseurs emprunteurs pour que des prêteurs leur confient leurs capitaux, pendant toute la durée d'un projet c'est à dire de leur prêt. Les 2.5 % reflètent le prix supplémentaire que les emprunteurs doivent payer, pour tenir compte de l'augmentation moyenne des prix attendue pendant la durée de leur prêt, pour que les prêteurs gardent constante la valeur de leur capital initial, en dehors de toute rémunération de ce capital. Le prêteur risque donc son capital pendant la durée du prêt pour une rémunération 6%, qui se décompose en 3.5% et un risque inflation de 2.5%.

En 2005, le taux moyen des prêts à 10 ans sur les marchés financiers Européens est de 4.2% avec une estimation d'inflation de 2%. Le taux réel est donc de 2.2%.

En d'autres temps, le taux du marché monétaire était de 8-9% comme c'était le cas en France en 1992 avec le même taux moyen d'inflation annuel estimé de 2,5 %, le taux d'intérêt en termes réels était alors de 6.5 %.

Depuis la monnaie unique européenne, l'Euro, c'est la banque centrale européene BCE qui fixe les taux d'intérêt. Le lien suivant donne ces taux au jour d'aujourd'hui.

Structure de taux

Taux courts (Euribor European Interbank offered rate). Et voir ici l'historique des taux Euribor.

Taux longs TEC 10 taux moyen des emprunts d'État à 10 ans (France Trésor). Et voir ici l'historique du TEC10.

On voit que les taux longs (10ans) en France sont de 4.25% en sept 2007. En ce qui concerne l'inflation, on trouvera les données nécessaires dans divers sites web dont http://www.nationmaster.com Il est de 2% pour la zone Euro fin 2003, ce qui donne un taux réel de 2%.

Dans les conditions économiques qui prévalent à un moment donné, le TRI d'un projet doit être au moins égal au taux d'intérêt en termes réels (par exemple 2% en 2003, 3.5% en 1995 ou 6.5% en 1995). Ce taux correspond à la rémunération minimum que l'on peut attendre sur le marché des capitaux, pour un capital investi dans un projet donné. En fait comme on envisage une durée de l'ordre de 20 ans, il faut estimer une valeur moyenne sur l'ensemble de la période. C'est pourquoi les institutions financières appliquent des taux plus élevés qui tiennent compte de leurs frais de gestion et de leur appréciation des risques.

Ce taux varie d'un pays à l'autre et dans le temps, en fonction des conditions économiques, c'est à dire des politiques suivies dans les différents pays pour stimuler ou ralentir leurs économies et de l'appréciation par les marchés financiers, des perspectives d'évolution de ces conditions économiques. Le tableau ci-après montre par exemple les taux des principaux pays en 1992.

	France	Allemagne	USA	Japon
taux du marché	8.5%	8.0%	7.0%	5.0%
estimation risque inflation	2.5%	4.0%	1.8%	1.7%
taux minimum en termes réels	6.0%	4.0%	5.2%	3.3%

Mais en mai 2005 les taux longs sont les suivants (taux à 10 ans).

En fonction des monnaies qui entrent dans la constitution des coûts et de leur poids respectifs, et en fonction de la durée du projet et des perspectives économiques, on établit une estimation du taux minimum, combinaison des taux indiqués ci-dessus. Ce taux minimum sert alors de référence absolue au TRI calculé pour un projet.

Pour la suite de cette étude, on considérera un taux minimum de 5% combinaison de 40% France, 44% Allemagne, 15% USA et 1% Japon et de l'évolution économique prévue fin 2003.

TRI: Taux objectif

Quel que soit le taux d'intérêt en termes réels auquel on parvient, il est souhaitable que le TRI soit supérieur à celui-ci, pour tenir compte de risques et d'aléas inhérents d'un projet plus ou moins difficiles à apprécier, ainsi que de risques propres à la branche et au secteur concernés, c'est à dire le métal ou la substance minérale et sa filière.

On peut ainsi considérer que le TRI objectif comporte au moins de 3% en sus du taux minimum pour tenir compte de risques et aléas propres au projet, et 3% encore en sus pour tenir compte de risques de la branche et du secteur.

Enfin, il est souhaitable que le TRI objectif comporte une part supplémentaire pour permettre à l'entreprise de constituer des réserves monétaires pour suivre le progrès technologique et les innovations dans sa branche et contribuer à la croissance économique du pays.

Un exemple frappant à cet égard est celui des processeurs dans les technologies de l'information et de la communication. La loi de Moore (du nom d'un des fondateurs de la société Intel, dit que la capacité des processeurs double tous les 18 mois. Il faut donc qu'une partie des équipements ait cette durée de vie, ce qui implique des investissements nouveaux fréquents et de gros efforts pour la recherche et développement.

Le tableau ci-après montre le calcul d'un taux objectif, à partir de taux de marché observés en 1992 et 1995 en France:

	1992	1995
taux du marché	8.5%	6.5%
estimation risque inflation	2.5%	2.0%
taux minimum en termes réels	6.0%	4.5%
risques projet	3.0%	3.0%
risques branche/secteur	3.0%	3.0%
TRI objectif	12.0%	10.5%

Dans l'exemple cité, le TRI est de 13.8% c'est à dire qu'il est plus élevé que le taux objectif de 1995 (10.5%), et celui de 1992 (12%). Le gouvernement français a adopté en 1994 et en 1995 une politique de relance prudente de l'activité économique pour lutter contre le chômage. Cette politique a pour effet de réduire le taux d'intérêt minimum et le TRI objectif de projets, donc d'encourager l'investissement.

L'appréciation du TRI d'un projet par rapport au TRI objectif doit s'apprécier au cas par cas selon les incertitudes et les risques susceptibles d'affecter le projet et la plus-value attendue. On considère qu'un écart de 6-8 points % est un objectif raisonnable. Un projet dont le TRI est de 10-12% peut donc être évalué positivement.

Dans les cas limites, et pour évaluer un projet d'investissement positivement selon le critère du TRI objectif, on doit tenir compte de tous les facteurs possibles. C'est ainsi qu'on peut être amené à considérer une valeur résiduelle des installations et des équipements investis en fin de période, dans la mesure où ils peuvent servir pour poursuivre l'activité au-delà. Il s'agit toutefois d'un facteur non strictement monétaire; c'est pourquoi il est recommandé de l'envisager seulement en variante, à une solution de base sans valeur résiduelle.

Le mode de calcul du TRI nécessite que la série à laquelle il s'applique, comporte des valeurs négatives au début (les investissements). S'il n'y a pas de valeurs négatives, le calcul du TRI devient impossible. Cela se produit généralement pour les projets d'extension ou de modernisation d'entreprises existantes déjà en opération. Il faut alors compter comme valeur de départ la situation nette de l'entreprise, comme s'il s'agissait d'un investissement initial. Ce sont en effet ces fonds immobilisés qui permettent à l'entreprise de fonctionner et de générer des bénéfices.

En variante à ceci, on peut calculer la valeur qu'il faudrait donner à l'entreprise pour qu'un acheteur éventuel réalise un objectif de taux de rentabilité, par exemple le TRI objectif de 12%. Par rapport à la valeur comptable de l'entreprise, cette valeur correspond alors à un décôte ou discount, qui tient compte de la situation existante et des perspectives futures.

Comparaison de projets selon le critère du TRI

Le TRI permet de comparer des projets concurrents ou des variantes d'un même projet. Un projet à TRI plus élevé est plus intéressant qu'un projet à TRI plus faible, si l'on considère ce seul critère d'appréciation.

Par exemple, pour un projet (projet B) dont l'investissement initial est de 150 millions US$ et la marge brute annuelle sur 20 ans de 20 millions US$, le TRI est de 10.8 % Voir figure. Il faut noter qu'à une durée d'évaluation plus courte, correspond un TRI plus faible. Dans l'exemple qui vient d'être cité, si la durée d'évaluation du projet était de 15 ans au lieu de 20, le TRI serait de 9.2 %, à moins que la marge brute ne devienne 21.4 millions US$ au lieu de 20 millions US$; dans ce cas, le TRI resterait égal à 10.8 %. Plus la durée de vie du projet est courte, plus le revenu annuel doit être élevé.

Si on considère la dernière année de l'évaluation une valeur résiduelle, de 40 millions US$ par exemple, correspondant à la part non totalement amortie des équipements et installations, le TRI deviendrait 11.4 % au lieu de 10.8%.

Etudes de sensibilité

Les études de sensibilité consistent à modifier les prix, ou les coûts des intrants et du personnel et de voir l'effet de ces modifications sur le TRI. Ces études permettent aussi de tester la validité du modèle, car chaque simulation interpelle.

Limites du TRI

Le TRI permet d'apprécier la rentabilité d'un projet par un nombre unique; mais il ne renseigne pas sur le volume de la marge nette escomptée sur la période d'évaluation. On n'a donc pas d'idée sur la valeur créée, l'importance économique du projet c'est à dire sa contribution à la création de richesse.

On a cependant une certaine indication sur ce point s'il existe un écart positif entre le TRI et le taux de référence considéré ou en examinant l'échéancier complet et la série des marges annuelles nettes. Plus l'écart entre le TRI et le taux de référence est important, plus la VAN de la série des marges annuelles nettes est positive et élevée, ce qui dénote une création de richesse importante.

Un autre critique, c'est que le TRI ne permet pas d'apprécier si la capacité de production envisagée est satisfaisante ou non; ne pourrait-on pas augmenter la production ainsi que la marge nette annuelle? La méthode de la valeur actuelle nette (VAN) répond mieux à cette question.

retour sommaire

3. LA METHODE DE LA VALEUR ACTUELLE NETTE

La valeur actuelle nette

Comme indiqué précédemment, on calcule la valeur actuelle nette (VAN) de la série des marges annuelles nettes, c'est-à-dire la différence entre la marge annuelle brute et l'investissement initial, à un taux d'actualisation fixé, par exemple le d'intérêt minimum en termes réels.

Mieux encore, on peut étudier la variation de la VAN en fonction du taux d'actualisation; on fera varier le taux d'actualisation par exemple selon la série 0, 2, 4, 6... jusqu'à 20 %. On trace alors la courbe donnant la VAN en fonction du taux d'actualisation ( voir figure pour projets A et B).

La figure montre à l'évidence que le projet A est plus intéressant que le projet B (sa VAN est supérieure), tant que le taux d'actualisation, c'est à dire le taux d'intérêt minimum, reste inférieur à 16%.

Le taux d'actualisation auquel correspond une VAN de zéro est le TRI. C'est le taux obtenu au point d'intersection de la courbe de la VAN avec l'axe des abscisses. Dans l'exemple du projet A, le TRI est de 13.8%. Dans celui du projet B, il est de 10.4%. Le projet A est plus capital intensif que le projet B; il reste plus intéressant que B tant que le taux d'intérêt ne dépasse pas 16%.

Comparaison de projets selon le critère de la VAN

La méthode de la VAN permet de comparer des projets concurrents ou des variantes d'un même projet.

Si l'on considère un taux de référence de 8%, on voit que la VAN 8% du projet A est de 153M$ alors que celle du projet B n'est que de 33&M$. Revoir la figure pour les projets A et B.

Le projet A consomme plus de capitaux que le projet B mais il génère davantage de richesse économique.

Le projet A dégage une marge brute annuelle de 55M$ et une VAN 8% de 153M$, pour un investissement initial de 350M$. Le TRI est de 13.8%, soit 8.3% de plus que les taux de référence 8%. C'est de cet écart que résulte le surplus de richesse produit par le projet par rapport à un taux de référence 8% qui représente le coût de rémunération des capitaux investis.

Le projet B, moins consommateur de capitaux, assure une marge brute annuelle de 20M$, une VAN 8% de 33M$, pour un investissement initial de 150M$. Le TRI est de 10.8%, soit 2.8% de plus que le taux de référence 8%. Avec ce taux de référence, le projet B est donc moins générateur de richesse puisqu'il produit 153-33=120M$ de moins que le projet A.

Le projet A génère donc 5 fois plus de richesse que le projet B au taux de référence 8%; de plus, la VAN du projet A reste plus élevée que celle du projet B, tant que le taux d'intérêt reste inférieur à 16%. Ce n'est que lorsque le taux d'intérêt devient supérieur à 16% que la VAN du projet A devient plus faible que celle du projet B et dans ce cas, le projet B l'emporte sur le projet A. Mais il s'agit d'un avantage théorique et illusoire car les VAN des 2 projets sont négatives toutes les deux depuis que le taux d'intérêt a dépassé 13.8%, le TRI du projet A.

Tout ceci confirme le fait que l'augmentation des taux d'intérêt rend les projets à forte valeur d'investissement plus difficiles à justifier sur le plan financier et donc contribue à pénaliser les projets d'investissements en économie de marché.

Limites de la méthode de la VAN

La méthode de la VAN ne permet pas de mettre en évidence le solde de tous les comptes de l'entreprise, c'est-à-dire la plus-value monétaire qui est disponible annuellement pour assurer l'équilibre de son fonctionnement, particulièrement le service de la dette (remboursement de capital et d'intérêts des emprunts contractées). En effet, on doit s'assurer que le projet maintient à tout moment l'équilibre financier de l'entreprise et que les sources de financement envisagées sont suffisantes pour cela. Si tel n'était pas le cas, l'entreprise serait en difficulté financière et devrait faire appel à des sources extérieures de financement. Celles-ci peuvent lui être refusées, ou être trop chères ou n'être attribuées qu'à des conditions qui lui feraient perdre son autonomie. Dans le cas extrême, l'entreprise pourrait être amenée à se restructurer voire à cesser son activité.

Le risque de déséquilibre financier est particulièrement dangereux au début du projet, quand les importantes dépenses d'investissements initiaux sont engagées et que la production n'est pas encore effective. La méthode du tableau financier, plus complète, permet de répondre à cette question.

Toutefois, l'écart entre le TRI et le taux de référence est un indicateur précieux de la capacité du projet à couvrir les frais financiers liés aux emprunts. Mieux, on peut calculer le taux moyen de tous les emprunts, en combinant leurs caractéristiques (taux d'intérêt, durée de remboursement dont années de différé).

On peut alors considérer la part des investissements couverte par ces emprunts et la part restante couverte par l'entreprise, et calculer la rentabilité de cette part restante, la combinaison des deux correspondant au TRI du projet. Un exemple de calcul est donné ci-après:

retour sommaire

4. LA METHODE DU TABLEAU FINANCIER

On construit l'échéancier des sources et emplois de fonds du projet à l'aide des tableaux financiers suivants. Le diagramme 1 précédemment indiqué permet de comprendre le processus d'établissement de ces tableaux.

- ventes = production, valorisée par les prix de vente unitaires

- excédent brut d'exploitation = ventes moins coûts de production directs (intrants et personnel)

- résultat d'exploitation = excédent brut d'exploitation moins autres coûts moins impôts directement liés au projet (taxes sur importations, royalties, redevances, etc.)

- marge brute = résultat d'exploitation, moins investissements (initiaux et de renouvellement)
(permet le calcul d'un TRI et d'une VAN)

- bénéfices taxables = résultat d'exploitation moins amortissements, moins intérêts d'emprunts

- résultat net d'exploitation = bénéfices taxables moins impôts sur bénéfice

- sources des fonds = résultat net d'exploitation plus amortissements plus apports de fonds propres plus emprunts

- emplois de fonds = investissements plus remboursements de capital des emprunts

- surplus monétaire annuel = sources des fonds moins emplois de fonds

- surplus monétaire cumulé

Le surplus monétaire cumulé doit rester positif pour que le projet soit viable financièrement.

Pour que surplus monétaire cumulé reste positif, il faut éventuellement ajuster les sources de financement, en tenant compte toutefois d'un ratio fonds propres/emprunts soit acceptable. Ce ratio est généralement de ½, c'est à dire que les fonds propres sont d'au moins un tiers du total fonds propres+emprunts. Ceci conduit à ce que le plus petit surplus monétaire cumulé soit nul ou presque nul. Cet ajustement des ressources financières est particulièrement important au cours des premières années du projet.

On observera que la méthode du tableau financier permet aussi de calculer le TRI et la VAN. L'exemple complet suivant donne un aperçu de cette méthode.

L'établissement des tableaux financiers présente les points supplémentaires suivants par rapport aux calculs du TRI et de la VAN:

- il faut calculer les amortissements des équipements et installations correspondant aux investissements

- il faut calculer les intérêts des emprunts et les remboursements de capital

retour sommaire

5. LA METHODE DU TEMPS DE RETOUR SUR INVESTISSEMENT ET DU TAUX DE RENTABILITE EXTERNE

Temps de retour sur investissement

A cause des incertitudes et des risques de l'avenir, un investisseur souhaite que la période de temps où il est soumis aux risques commerciaux et techniques soit la plus courte possible. Il cherche donc à récupérer son investissement aussi vite que possible. Le temps de retour est donc le nombre d'années nécessaire pour récupérer le montant de l'investissement initial avec la marge brute annuelle.

Une variante consiste à raisonner sur les valeurs actuelles au taux de référence retenu de 8%, des marges brutes annuelles et de l'investissement initial. On obtient alors un temps de retour sur valeurs actualisées; ce dernier est en général 40 à 50% plus élevé que le temps de retour non actualisé. Ceci permet donc une meilleure utilisation du temps de retour comme paramètre d'évaluation.

Les figures 6 et 7 montrent clairement le mode de calcul de ces temps de retour pour le projet A.

On voit que le temps de retour du projet A est de 8 ½ ans avec des valeurs non actualisées et de 11 ½ ans avec des valeurs actualisées.

Par comparaison, les figures 8 et 9 donnent les mêmes résultats pour le projet B. On voit que le temps de retour du projet B est de 8 ½ ans avec des valeurs non actualisées et de 13 ans avec des valeurs actualisées.

La méthode du taux de rentabilité externe

La méthode du taux de rentabilité externe nécessite d'abord de définir ce qu'on entend par valeur ultime (VU) d'un revenu futur et par valeur ultime nette (VUN) d'une série de revenus futurs

La valeur ultime (VU), en fin de période d'évaluation d'un projet, d'un revenu de 100 millions US$ attendu par exemple dans l'année 8, est le montant du capital et des intérêts composés qu'on obtiendrait si l'on plaçait en fin d'année 8 les 100 millions US$, jusqu'à la fin de la période d'évaluation du projet. On considère comme taux d'intérêt pour ce placement, le taux de référence de 8%.

Pour un taux d'intérêt de 8%, la VU de 100 millions US$ attendus par exemple dans l'année 8, est de 252 millions US$. La VU de 100 millions US$ attendus par exemple dans l'année 15 serait de 147 millions US$ (figure 10).

La valeur ultime nette (VUN) d'une série de revenus futurs est la somme des VU de chaque terme annuel Ainsi pour le projet A, la VUN 8% est de 2060 millions US$. Elle est de 829 millions US$ pour le projet B.

Les équations de calcul ci-dessous et les figures 10 et 10bis explicitent le concept et le mode de calcul de la VU et de la VUN dans le cas de l'exemple cité.

Le taux de rentabilité externe (TRE) est alors le taux d'intérêt tel que si l'on plaçait le même montant que l'investissement initial (actualisé à l'année ) jusqu'en fin de période d'évaluation, le capital et l'intérêt obtenu serait égal à la VUN ci-dessus définie. Ainsi pour le projet A, le TRE est de 9.5% Il est de 8.9% pour le projet B.

Le projet A dégage donc une rentabilité supérieure de 1.5% au taux de référence (externe au projet), de 8%. Le projet B dégage une rentabilité supérieure de 0.9% à ce même taux de référence externe.

Le taux de rentabilité externe a l'intérêt de mettre le projet en concurrence avec l'alternative de placer le montant de l'investissement prévu, à un taux de rentabilité de 8%.

retour sommaire

6. SYNTHESE DES METHODES DU TRI ET DE LA VAN

Rappel de la méthode du TRI

La méthode du TRI permet d'apprécier la rentabilité d'un projet à l'aide d'un estimateur unique, c'est-à-dire le taux d'actualisation pour lequel, la valeur actuelle de la marge nette annuelle est nulle. Le TRI représente donc le taux de rémunération attendu de l'investissement initial, c'est-à-dire du capital immobilisé dans le projet.

Le TRI ne donne pas d'indication sur le volume de la marge nette dégagée par le projet au cours de la période d'évaluation. Il faut pour cela apprécier l'écart entre le TRI et le taux d'intérêt de référence. Selon quels critères doit on faire cette appréciation et quel écart positif doit on chercher à obtenir ? En effet, un TRI qui ne serait pas plus élevé que le taux de référence ne donnerait qu'une rémunération minimum des capitaux engagés et ce, à condition que les risques et aléas soient négligeables; cette rémunération ne permettrait donc pas à l'entreprise de constituer de réserves pour assurer sa sécurité contre les aléas de la conjoncture économique à moyen et à long termes, ni de contribuer à la croissance économique du pays.

Rappel de la méthode de la VAN

La méthode de la VAN permet de caractériser un projet par le volume de la marge nette dégagée, sous la forme d'une valeur actuelle nette à différents taux d'actualisation. En adoptant pour taux d'actualisation le taux d'intérêt de référence, on obtient alors l'estimation de la VAN du projet à ce taux qui correspond au taux du marché monétaire en monnaie constante. La méthode de la VAN inclut par ailleurs le TRI puisque celui-ci est le taux d'actualisation pour lequel la VAN = 0. L'appréciation du projet dépend donc du taux de référence considéré et de sa relation avec le taux d'intérêt moyen du marché monétaire, estimé sur la durée d'évaluation du projet.

Calculs manuels et simplifiés

Une présentation simplifiée des méthodes du TRI et de la VAN, est la suivante :

- soit "" un investissement initial et M la marge brute annuelle que permet de dégager cet investissement, marge que l'on supposera constante (on peut raisonner sur une valeur moyenne annuelle).

- la valeur actuelle d'une marge brute dégagée chaque année pendant 20 ans, peut se calculer à l'aide d'une table de la valeur actuelle nette d'un revenu de en fonction du taux d'actualisation et de la durée (voir Table). Il suffit de multiplier la marge brute annuelle par le coefficient approprié lu dans la table, pour obtenir la valeur actuelle correspondante. Pour que le résultat des calculs soit le plus approché possible, on considère que la marge brute est dégagée à partir de l'année 3 et que l'investissement initial est dépensé aux années précédentes 2 et 1. On calcule donc les valeurs actuelles à l'année 3. On peut aussi considérer l'année de départ du projet comme 1, et les années d'investissement comme négatives c'est à dire dans ce cas -1 et -2.

On traite successivement les recettes et l'investissement:

Recettes

Par exemple pour le projet A, la marge brute annuelle est de 55 millions US$ à partir de l'année 3. La VA d'un revenu de 1 à 8 % pendant 20 ans, sooit année 3 à 22, lue dans la table, est de 10.20 et celle des 2 premières années est de 1.79. La valeur actuelle d'un revenu annuel de 55 millions US$ des années 3 à 22 est donc:

55x(10.20-1.79)=463 millions US$.

Investissements

La valeur de l'investissement initial est de 150 et 200 millions US$ les années 1 et 2. La (table ci-contre) donne la valeur actuelle d'un montant de 1 en fonction du taux et de l'année de dépense. On calcule aisément que la valeur actuelle à 8% de l'investissement ci-dessus est de 310 millions US$.

soit, 0.93x150+0.86x200=310

6.3.3. Calcul de la VAN 8%
Il reste donc une VAN 8 % de:

463-310=153 millions US$.

On retrouve donc bien la VAN 8 % du projet A telle que calculée précédemment:

Faut-il maximiser le TRI ou la VAN ?

A ce stade, on peut se poser la question suivante : lors de la conception d'un projet, comment peut-on maximiser le TRI et/ou la VAN du projet au taux de référence envisagé. Une représentation graphique du TRI et de la VAN permet de comprendre et de répondre.

Représentation graphique

On peut représenter graphiquement le TRI et la VAN de projets de la manière suivante. Soit "M" la marge brute moyenne annuelle dégagée par un investissement "I", marge que l'on suppose constante.

La marge brute annuelle croît lorsque l'investissement augmente, en raison de la productivité du facteur capital. Mais la productivité du capital est soumise à la loi des rendements décroissants, comme les autres facteurs de production. Si l'on représente la marge brute moyenne annuelle en fonction de l'investissement, la courbe correspondante croît fortement avec l'investissement puis la courbe s'infléchit, passe par un maximum, et se met ensuite à décroître.
(voir cette courbe).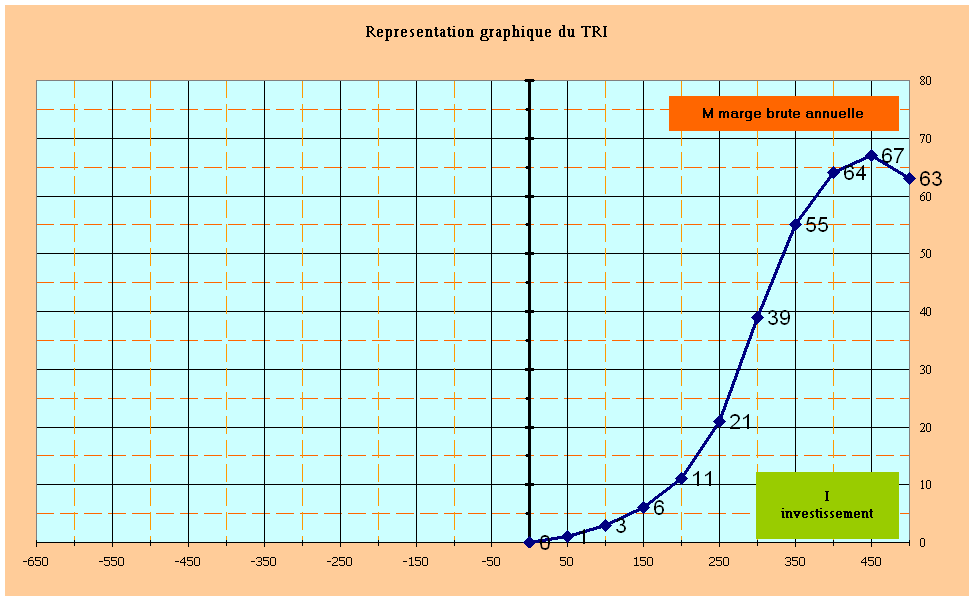

La VA d'une marge brute moyenne annuelle sur 20 ans au taux d'actualisation de 8% par exemple, est le produit de cette marge brute par 9.82 (voir VA d'un revenu de 1 pendant 20 ans à 8%). La valeur actuelle nette VAN, est la VA de la marge brute moins l'investissement.

Dans le cas où I=350 et M=55, VA=55x9.82=540; et VAN=540-350=190.

Graphiquement, la VA de la marge brute "M", au taux de 8%, peut se représenter par un segment sur l'axe des abscisses à partir de la projection sur l'axe des abscisses du point 55,350 soit 540 vers la gauche, ou 190 depuis l'origine (190+350=540). Pour la commodité d'apparence de la courbe, je reporte les investissements vers la droite donc en positif, et les revenus vers la gauche donc en négatif. Ce segment est la projection sur l'axe horizontal d'un segment incliné d'un angle α, tel que la tangente de α est égale à 55/540, ou 1/9.82 (1/VAN de 1 à 8% sur 20 ans), soit un angle d'environ six degrés.

On peut donc représenter le taux d'actualisation de 8%, par un angle qui correspond à la valeur actuelle d'un revenu annuel de 1 au taux de 8%. Pour que la représentation graphique soit plus lisible, il est commode d'adopter une échelle différente pour les marges brutes en ordonnées, (par exemple une échelle 10 fois plus grande qu'en abscisses). Il en résulte que l'angle apparent sur le graphique est d'environ 45 degrés.
(voir courbe)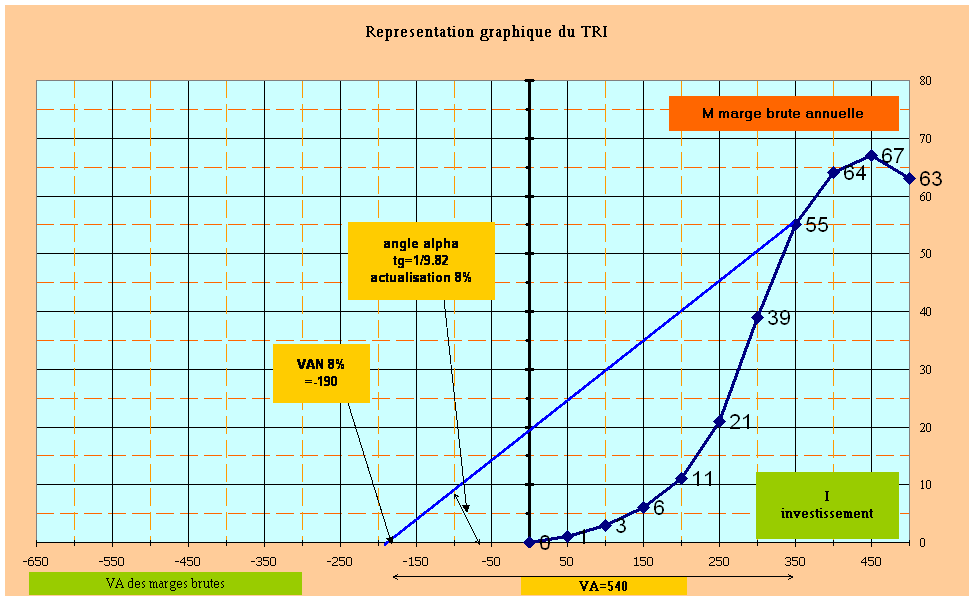

Exemple pratique

La figure 11 montre la courbe de la marge brute annuelle en ordonnées, en fonction de l'investissement initial en abscisses. A la marge brute annuelle de 55 millions US$ correspond le point M de la courbe et l'investissement initial de 350 millions US$. La VA de la marge brute à 8% est obtenue en traçant à partir de M le segment MA qui coupe l'axe des abscisses à -450 millions US$. Au segment MO correspond le TRI.
(voir courbe)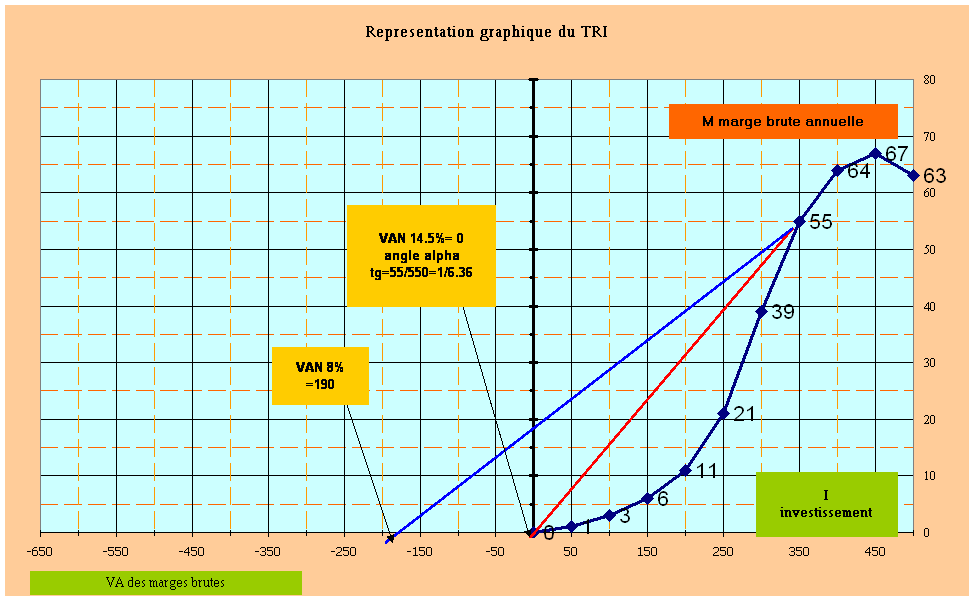

Cela étant, lors de la conception du projet, si l'on cherche à maximiser la valeur produite, il faut s'efforcer de maximiser la VAN au taux de référence choisi de 8% et non le TRI qui revient à maximiser le rendement du capital investi.

La figure montre qu'on obtient le TRI maximum en traçant la tangente à la courbe à partir de l'origine O. L'investissement initial est alors 380 millions US$, et la marge brute annuelle de 62 millions US$. La VAN 8% correspondante, est 609 millions US$.

La VAN 8% maximum, est obtenue en menant la tangente à la courbe correspondant au taux d'actualisation de 8%. L'investissement initial est 400 millions US$ et la marge annuelle brute est 64 millions US$. La VAN 8% maximum est de 628 millions US$ et le TRI correspondant est légèrement plus faible.

Tant que le TRI d'un accroissement marginal d'investissement (TRI marginal) reste supérieur au taux de référence de 8 %, on peut encore accroître la VAN 8% donc la richesse produite par le projet. La VAN 8% maximum est obtenue quand le TRI marginal d'un investissement additionnel est de 8%. On peut vérifier que lorsqu'on déplace M vers la droite, le TRI marginal reste supérieur à 8% tant que qu'on n'a pas atteint le point de tangence. Quand on atteint le point de tangence, le TRI marginal s'abaisse à 8% et on est donc parvenu au maximum de la VAN 8%.

NB: Dans l'exemple choisi, les deux valeurs TRI maxi et VAN maxi sont pratiquement confondus; il n'en est pas toujours ainsi.

retour sommaire

7. RENTABILITE ECONOMIQUE D'UN PROJET

Valeur ajoutée et balance des paiements

La rentabilité économique d'un projet permet d'apprécier l'intérêt du projet pour le développement économique du pays. La valeur ajoutée, différence entre la production vendue et les intrants ou achats extérieurs, constitue la contribution de l'entreprise au produit intérieur brut (PIB) du pays. Par ailleurs, la balance des paiements du projet contribue à la balance des paiements du pays. Le calcul de la rentabilité économique d'un projet nécessite donc de calculer sa valeur ajoutée et sa balance des paiements.

Correction des distorsions de prix

En général il faut corriger au préalable, les ventes et les coûts notamment ceux des intrants, dans la mesure ou ceux-ci subissent des distorsions en plus ou en moins, par suite de subventions, de droits de douane ou de taxes. On corrigera les prix de vente unitaires pour qu'ils correspondent au prix de marché international FOB, compte tenu des frais de transport jusqu'à la frontière. On corrigera les coûts d'intrants pour qu'ils correspondent aux coûts CIF des produits disponibles sur le marché international, c'est-à-dire compte tenu des frais de transport jusqu'à la frontière.

Balance des paiements du projet

Pour établir la balance des paiements du projet, on calculera la différence entre les revenus en devises et les dépenses en devises, y compris les remboursements de capitaux étrangers et les paiements d'intérêts liés. Ces données se trouvent dans le tableau financier des sources et emplois de fonds. L'étude de la rentabilité économique d'un projet nécessite donc de conduire l'étude financière par la méthode des tableaux financiers.

retour sommaire