W artykule Efekt Allaisa i ciemna materia zaproponowałem koncepcję wyjaśnienia płaskości krzywej rotacji galaktyk przy pomocy Falowej teorii Grawitacji a dokładniej ze zwielokrotnionego efekty Allaisa. Efekt ten polega na wzmocnieniu oddziaływania grawitacyjnego między dwoma masami (Słońce i Ziemia) przez orbitującą trzecią masę (Księżyc) w obszarze cienia. Rozważania moje dotyczyły galaktyki spiralnej w której jądro przysłaniały gwiazdy wewnętrzne, na skutek ruchu orbitalnego ze zbliżoną prędkością ale przy różnych promieniach, co daje efekt mijania. Wzmocnienie grawitacji wynik wypadkowej efektu Dopplera ruchu do i od źródła,
ΔΔg= g (V/c+2(V/c) ² ) / (1+V/c)- ǀg (-V/c+2(V/c) ² )/(1-V/c) ǀ
ΔΔg=2(V/c)^2/(1-(V/c)^2) Dla V<<c ΔΔg=2(V/c)/^2
g(1+2(V/c)^2) ^N=5g
N= ln(5) / ln(1+2(V/c)^2 =1,81E 8
g – Przyspieszenie grawitacyjne, V- Prędkość mijania najbliższych gwiazd od Słońca 20 km/s, c-Prędkość światła. N Liczba orbitujących mas wchodzących w interakcję
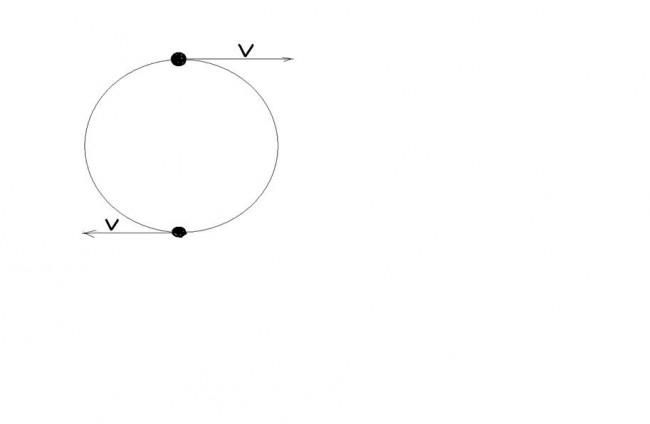
Po analizie tego modelu okazało się że interakcja galaktyki jako całości daję zdecydowanie większy przyrost ciążenia.. Jako że problem jest niezwykle skomplikowany zacznę od dwóch gwiazd orbitujących prędkością V które potraktujemy jako układ gwiazd podwójnych rotujących wokół centrum galaktyki ( a galaktykę składającą się z setek miliardów takich układów) , dzięki czemu uzyskujemy interakcję całej galaktyki.
Efektywna prędkość mijania w takim układzie wyniesie 2V. a wiec powyższe równanie będzie miało postać
g(1+8(V/c)^2) ^N=5g
N= ln(5) / ln(1+8(V/c)^2 =3,42 E 5
g– Przyspieszenie grawitacyjne, V- Prędkość orbitalna gwiazd 230 km/s, c-Prędkość światła. N Liczba orbitujących mas wchodzących w interakcję
Kolejnym mechanizmem dającym wkład do wzmacniania grawitacji w galaktykach spiralnych jest interakcja orbitujących gwiazd dysku z gwiazdami zgrubienia galaktycznego, którego orbity gwiazd mają przeróżne konfiguracje w stosunku do płaszczyzny dysku w tym prostopadłe. Względna prędkość mijania w prostopadłych orbitach wyniesie √2 V. Dla prędkości orbitalnej V=230 km/s (zakładając że obie mają prędkość zbliżoną) prędkość mijania wyniesie 325 km/s
N= ln(5) / ln(1+4(V/c)^2 =6,84 E 5
Biorąc pod uwagę że w naszej Drodze Mlecznej liczbę gwiazd szacuje się na 2E11 to liczby orbitujących mas wchodzących w interakcję są mniejsze o wiele rzędów dla trzech wymienionych mechanizmów i kombinacji, a myślę że wszystkie wpływają na dynamikę ruchu galaktyk W galaktykach karłowatych nie obserwuje się płaskości krzywej rotacji bo składają się z kilku milionów gwiazd i te efekty będą zbyt małe do obserwacji. Problemem są gromady galaktyk które składają się, co najwyżej z kilku tysięcy galaktyk, a mimo to, krzywe rotacji nie pasują do praw Keplera. Te gromady wypełnia gęsty i gorący ośrodek miedzygalaktyczny o masie porównywalnej z masą galaktyk, który z cała pewnością rotuje wokół środka grawitacyjnego całej gromady a zachodzące tam efekty grawitacyjne są analogiczne jak w galaktykach spiralnych. Wykonanie takich obliczeń czy też symulacji komputerowych będzie nie lada wyzwaniem ponieważ każdej gwieździe w galaktyce i każdej cząstce ośrodka międzygalaktycznego trzeba nadać położenie, pęd, ale również rozciągłość przestrzenną co zwielokrotni liczbę rzędów bajtów informacji do przetworzenia.
Iwanowski Krzysztof